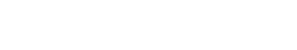CH3COOH or Acetic acid
OAc- is the shortcut for CH3COO- or the Acetate ion, the conjugate base of Acetic acid
1) VHCl = 0 mL (before addn of HCl)
Change of Concentrations Due to Dilution (M1V1 = M2V2)
[OAc-] = 0.100 M
50 mL
[OAc-] = (0.100)(50)/95 = 0.0526 M
[HOAc] = 0.100 M
45 mL
[HOAc] = (0.100)(45)/95 = 0.0474 M
Vtotal = 95 mL
You took 30.00 mL of the buffer:
[OAc-] = 0.0526M
30 mL
[OAc-] =
(0.0526)(30.00)
=
0.0522 M
30.25 + 0
[HOAc] = 0.0474 M
30 mL
[HOAc] =
(0.0474)(30.00)
=
0.0470 M
30.25 + 0
Plug these values in the ICE Table:
HOAc + H2O < = > H3O+ + OAc-]
Initial 0.0470 M 10-7 0.0522 M
Change -x +x +x
Equilibrium 0.0470 - x x 0.0522 + x
Then into the equilibrium expression:
Ka = [H3O+][OAc-] = 1.76 x 10-5 = x (0.0522 + x)
[HOAc] 0.0470 - x
5% of 0.0474 = 2.37 x 10-3
assume x is less than this value
1.76 x 10-5 = x (0.0522 )
0.0470
Solving for x = [H3O+]
[H3O+] = 1.58 x 10-5
pH = - log [H3O+] = 4.80 M
2) Addn of 0.100 M HCl
Calculate these concentrations for each volume of acid added corresponding to the increments added in Table 12.2 in the manual:
[OAc-] = 0.0526M
30 mL
[OAc-] =
(0.0526)(30.00)
30.25 + VHCl added
[HOAc] = 0.0474 M
30 mL
[HOAc] =
(0.0474)(30.00)
30.25 + VHCl added
Remember that the volumes are additive (i.e., the volume of HCl added after the second addition of the acid is 0.50 + 1.00 = 1.50 mL, third time is 1.50 + 1.50 = 3.0 mL and so on )
You are adding an acid to the buffer, calculate [HCl] for each volume of acid added:
[HCl]
=
0.100 M
x
V HCl added
30.25 + VHCl added
You will be adding this value to [HOAc] and subtracting it from [OAc-] in the ICE table:
Example: After addition of 0.50 mL of HCl, [HCl] = 0.00163
HOAc + H2O < = > H3O+ + OAc-]
Initial 0. 0462 + 0.00163 10-7 0.0513 - 0.00163
Change -x +x +x
Equilibrium 0.0478 - x x 0.0497 + x
Then into the equilibrium expression:
Ka = [H3O+][OAc-] = 1.76 x 10-5 = x (0.0497 + x)
[HOAc] 0.0478 - x
5% of 0.0478 = 2.39 x 10-3
assume x is less than this value
1.76 x 10-5 = x (0.0497 )
0.0478
Solving for x = [H3O+]
[H3O+] = 1.69 x 10-5 < 2.39 x 10-3
pH = - log [H3O+] = 4.77 M
Notice that the pH did not change that much compared to the original pH of 4.80 unlike the degassed water where the pH dropped from 7.0 to 2.1 with the addition of 0.25 mL of HCl.
Also, notice that the addition of an acid decreases the pH.
Part C: Addition of NaOH to Degassed Water
1) Without the base, the pH should be close to 7.0, [OH-] = 10-7