pezenfuego
Active Member
I will begin by accrediting beaslbob for the original idea. His analogy involved galloping elephants, which were used as a general unit of measure. At first Galloping Elephants were used to represent levels that we wish to reach 0 (nitrates, phosphates, ammonia, nitrites...). Or in other words, Galloping Elephants represented levels that are not present in the change water. But now the analogy will be extended and we will represent any aquarium parameter with Galloping Elephants.
To begin, we have to understand what a galloping elephant represents. In the aquarium, we don't test for the number of something. Instead we test for a concentration of something. For example, some units we are familiar with are parts per million (ppm) and parts per thousand (ppt). This represents one part solute for every (million, thousand, billion) parts solvent (water). Since everything in the water is equally distributed, it doesn't matter what volume of water you have. But for simplicity, we will assume that Galloping Elephants do not represent a concentration of something, but the exact number of that something. In actuality, this affects nothing. In my opinion, this simply makes the whole process easier to understand and visualize. So if we are designating Galloping Elephants to be calcium, then 100 Galloping Elephants translates to 100 calcium molecules.
DISCLAIMER: The following formula uses assumptions and does not account for every variable and biological process in the aquarium. But do not take this disclaimer as indicating that the formula is useless. The formula accounts for ideal conditions and is extremely useful in understanding, conceptually, how important water changes are. In addition, we will be able to prove certain ideas that will be discussed later. It is possible, but not likely, that this formula can be used for estimating future conditions. However, for most hobbyists, this will not be the case.
So the question is this: "How important are water changes?" To answer this question we are going to begin with a few assumptions. To use the resulting formula, you will not need any sort of mathematical ability, but to follow the thread, you will need a very basic understanding of mathematical series.
Assumption:
1) The aquarist knows exactly how much water is in their system.
2) The aquarist has constant husbandry
3) Galloping elephants are equally distributed throughout the water (if this is not a fair assumption, then we are improperly testing our water levels).
4) Galloping elephants increase/decrease at a uniform rate (independent of water changes) that can be measured (the important part of this assumption is the increase/decrease portion. If they increase in such a way that is not uniform, this does not hinder the overall idea, but will render the formula itself useless).
5) Water changes are the only thing that can remove/add galloping elephants.
6) The value of Galloping Elephants in the water which is used for a water change (change water) is constant. (this is fair assuming the same salt and dosing procedure is used for every water change)
The bolded assumptions are assumptions that I deem unfair, which is the entire reason why this formula may not be used to make accurate predictions.
You can do this calculation for any measure of time. You can use days, months, years, seconds, minutes, etc., but each variable that relies on time must agree. To reduce confusion, we will do everything in terms of weeks assuming that water changes are done weekly. The formula will work just as well if you do water changes every day, month, or fortnight.
Variables:
n= the number of weeks that go by
r= rate that galloping elephants increases per week (note that this will be negative if the value decreases)
w= fraction of water that is replaced per unit time (This cannot be less than 0 or greater than 1)(0<=w<=1)
v=starting value of galloping elephants in the aquarium
h=number of galloping elephants in change water
an=number of galloping elephants after n weeks go by (this is always evaluated right after a water change)
an-1=number of galloping elephants after n-1 weeks go by
So the beginning part is rather confusing, so we will take several additional steps.
So we go through a typical week of water changes and look at what our galloping elephant count is. We start at week 0. How many galloping elephants are in the water? Well the initial value of galloping elephants is:

Okay, so that's our initial value. Now we wait a week. How many galloping elephants were added to the tank? If the tank increases/decreases in galloping elephants at a rate of r galloping elephants per week, then after one week we have r additional galloping elephants:
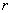
So after one week, how many galloping elephants do we have?
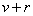
So this is prior to a water change. Now that we are ready to do our water change, we must first remove some water. We remove w percent of the water and therefore remove w percent of the galloping elephants. Thus, we remove this many galloping elephants:
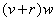
Now it is time to replace the water that was removed. This is a confusing part (potentially). Here is where the ambiguity between taking concentrations and taking numbers of galloping elephants becomes clear. Imagine that you have a tank (that happens to be the same size as your regular tank) that is filled with change water. The assumption was that there is a correct number of galloping elephants in this change water. So we take w percent of it and put it in our regular tank. That's how I look at it. Regardless, we are adding this many galloping elephants:
erfish.com/content/type/61/id/366456/" />
So we add all of this together and rearrange it a bit to get:
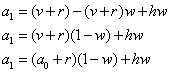
Notice that we replaced v with a0 that's because we defined the value of galloping elephants at 0 weeks to be v:

So now we calculate the value of galloping elephants at two weeks. We can just follow the same procedure as before, but now the initial value is a0 so we get this:
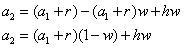
And the general form is pretty easy to see at this point:

But we can't have this in terms of an-1 because that is useless to us. So we find the pattern:
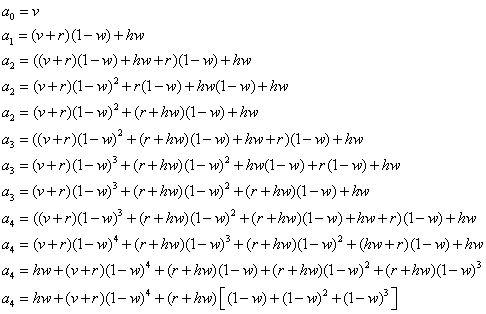
So now we have created a formula that can be written in terms of sigma:

But we don't want this in terms of sigma. It is difficult to think in terms of sigma. So we use the geometric series formula. I won't go through the trouble of proving it as you can easily ind a proof online if you are interested:
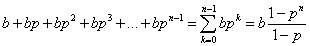
But you'll notice that this only works when we are evaluating the sum from 0 to n-1. Our equation goes from 1 to n-1. So we need to do a little math and find the value for this from 0 to n-1:
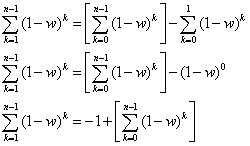
So let's replace that in our original formula:
/>
And we focus solely on the summation portion and solve:
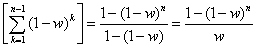
And then we plug it back in:
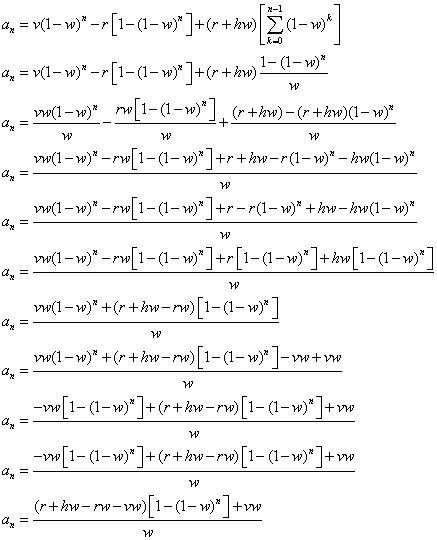
Okay, so this is our equation:
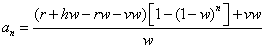
So the biggest question we want to answer is what will happen after a whole bunch of weeks pass by? What will our value of galloping elephants be? The best way to answer this is to look at what happens after an infinite number of weeks and water changes:
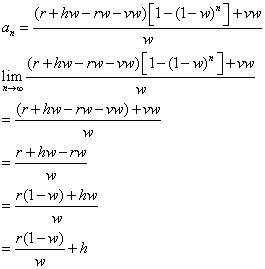
If you are confused as to how the term (1-w)^n dropped out of the equation, consider the fact that 1-w will always be a fraction since w cannot be greater than 1. When we raise a fraction to an infinite power, it goes to 0, always. So now we have another equation that we can use. Let's say that we want h galloping elephants after all of these water changes. After all, we do want h galloping elephants at all times. So we set the equation equal to h:
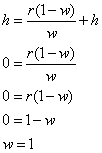
This shows that the only way to accomplish such a task is to do 100% water changes. We answered the question that was put forth. Assuming h is the ideal value of nitrates, the only way to get that value to 0 is by doing 100% water changes. Assuming h is the ideal value of pH, the only way to get that value to 8.2 is by doing 100% water changes. But remember, this is under the assumption that only water changes can add or remove galloping elephants. Which is untrue. This whole thread simply demonstrates that something other than water changes is necessary to keep your values in check indefinitely.
But what does this really tell us? Perhaps if I do a 1 percent water change every week indefinitely, I will end up with just 0.01 nitrates or 8.199 pH. The formula doesn't say that this cannot happen and I would be perfectly okay with that value for nitrates or pH. So we simply take the original equation that we got from taking the limit and we set it equal to something else. Here, we set it equal to h plus or minus some error. We will add the error and just assume that the error can be negative depending on what we define the galloping elephant as (also note that when r is negative, so is e):

So if we set the value of e equal to 0, then we get the need for a 100% water change. As your willingness to accept error increases, the size of the water change that you need to do decreases. If any equation is potentially useful, it is this one. estimating your value for r and using your accepted error is a great way to ballpark the size of the water change you should be doing. Another method would be to vary the size of your water changes such that you are adding the necessary elements back into the aquarium. For example, doing the occasional giant water change could really help your system. Water changes are an important part of the hobby. It is important that we understand them and use them accordingly.
-Cameron
To begin, we have to understand what a galloping elephant represents. In the aquarium, we don't test for the number of something. Instead we test for a concentration of something. For example, some units we are familiar with are parts per million (ppm) and parts per thousand (ppt). This represents one part solute for every (million, thousand, billion) parts solvent (water). Since everything in the water is equally distributed, it doesn't matter what volume of water you have. But for simplicity, we will assume that Galloping Elephants do not represent a concentration of something, but the exact number of that something. In actuality, this affects nothing. In my opinion, this simply makes the whole process easier to understand and visualize. So if we are designating Galloping Elephants to be calcium, then 100 Galloping Elephants translates to 100 calcium molecules.
DISCLAIMER: The following formula uses assumptions and does not account for every variable and biological process in the aquarium. But do not take this disclaimer as indicating that the formula is useless. The formula accounts for ideal conditions and is extremely useful in understanding, conceptually, how important water changes are. In addition, we will be able to prove certain ideas that will be discussed later. It is possible, but not likely, that this formula can be used for estimating future conditions. However, for most hobbyists, this will not be the case.
So the question is this: "How important are water changes?" To answer this question we are going to begin with a few assumptions. To use the resulting formula, you will not need any sort of mathematical ability, but to follow the thread, you will need a very basic understanding of mathematical series.
Assumption:
1) The aquarist knows exactly how much water is in their system.
2) The aquarist has constant husbandry
3) Galloping elephants are equally distributed throughout the water (if this is not a fair assumption, then we are improperly testing our water levels).
4) Galloping elephants increase/decrease at a uniform rate (independent of water changes) that can be measured (the important part of this assumption is the increase/decrease portion. If they increase in such a way that is not uniform, this does not hinder the overall idea, but will render the formula itself useless).
5) Water changes are the only thing that can remove/add galloping elephants.
6) The value of Galloping Elephants in the water which is used for a water change (change water) is constant. (this is fair assuming the same salt and dosing procedure is used for every water change)
The bolded assumptions are assumptions that I deem unfair, which is the entire reason why this formula may not be used to make accurate predictions.
You can do this calculation for any measure of time. You can use days, months, years, seconds, minutes, etc., but each variable that relies on time must agree. To reduce confusion, we will do everything in terms of weeks assuming that water changes are done weekly. The formula will work just as well if you do water changes every day, month, or fortnight.
Variables:
n= the number of weeks that go by
r= rate that galloping elephants increases per week (note that this will be negative if the value decreases)
w= fraction of water that is replaced per unit time (This cannot be less than 0 or greater than 1)(0<=w<=1)
v=starting value of galloping elephants in the aquarium
h=number of galloping elephants in change water
an=number of galloping elephants after n weeks go by (this is always evaluated right after a water change)
an-1=number of galloping elephants after n-1 weeks go by
So the beginning part is rather confusing, so we will take several additional steps.
So we go through a typical week of water changes and look at what our galloping elephant count is. We start at week 0. How many galloping elephants are in the water? Well the initial value of galloping elephants is:

Okay, so that's our initial value. Now we wait a week. How many galloping elephants were added to the tank? If the tank increases/decreases in galloping elephants at a rate of r galloping elephants per week, then after one week we have r additional galloping elephants:
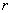
So after one week, how many galloping elephants do we have?
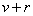
So this is prior to a water change. Now that we are ready to do our water change, we must first remove some water. We remove w percent of the water and therefore remove w percent of the galloping elephants. Thus, we remove this many galloping elephants:
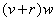
Now it is time to replace the water that was removed. This is a confusing part (potentially). Here is where the ambiguity between taking concentrations and taking numbers of galloping elephants becomes clear. Imagine that you have a tank (that happens to be the same size as your regular tank) that is filled with change water. The assumption was that there is a correct number of galloping elephants in this change water. So we take w percent of it and put it in our regular tank. That's how I look at it. Regardless, we are adding this many galloping elephants:
erfish.com/content/type/61/id/366456/" />
So we add all of this together and rearrange it a bit to get:
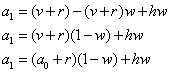
Notice that we replaced v with a0 that's because we defined the value of galloping elephants at 0 weeks to be v:

So now we calculate the value of galloping elephants at two weeks. We can just follow the same procedure as before, but now the initial value is a0 so we get this:
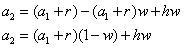
And the general form is pretty easy to see at this point:

But we can't have this in terms of an-1 because that is useless to us. So we find the pattern:
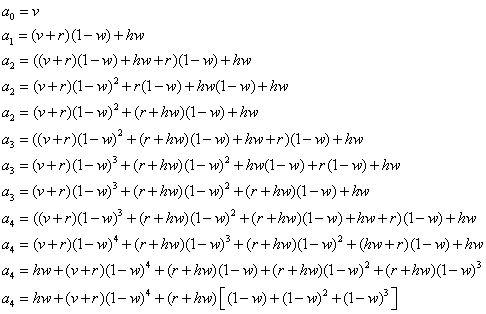
So now we have created a formula that can be written in terms of sigma:

But we don't want this in terms of sigma. It is difficult to think in terms of sigma. So we use the geometric series formula. I won't go through the trouble of proving it as you can easily ind a proof online if you are interested:
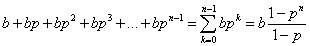
But you'll notice that this only works when we are evaluating the sum from 0 to n-1. Our equation goes from 1 to n-1. So we need to do a little math and find the value for this from 0 to n-1:
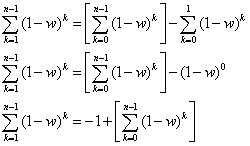
So let's replace that in our original formula:
/>
And we focus solely on the summation portion and solve:
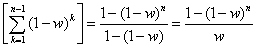
And then we plug it back in:
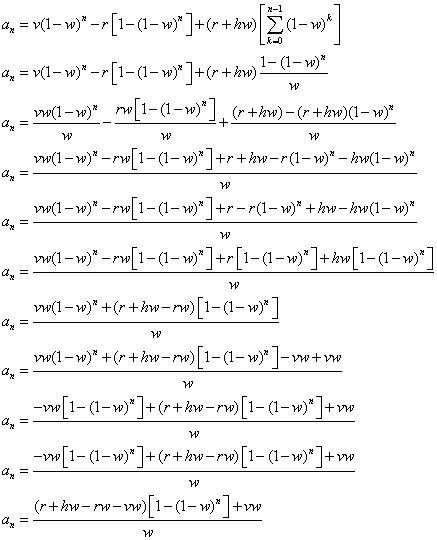
Okay, so this is our equation:
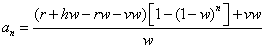
So the biggest question we want to answer is what will happen after a whole bunch of weeks pass by? What will our value of galloping elephants be? The best way to answer this is to look at what happens after an infinite number of weeks and water changes:
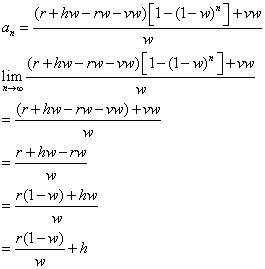
If you are confused as to how the term (1-w)^n dropped out of the equation, consider the fact that 1-w will always be a fraction since w cannot be greater than 1. When we raise a fraction to an infinite power, it goes to 0, always. So now we have another equation that we can use. Let's say that we want h galloping elephants after all of these water changes. After all, we do want h galloping elephants at all times. So we set the equation equal to h:
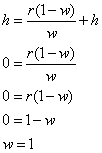
This shows that the only way to accomplish such a task is to do 100% water changes. We answered the question that was put forth. Assuming h is the ideal value of nitrates, the only way to get that value to 0 is by doing 100% water changes. Assuming h is the ideal value of pH, the only way to get that value to 8.2 is by doing 100% water changes. But remember, this is under the assumption that only water changes can add or remove galloping elephants. Which is untrue. This whole thread simply demonstrates that something other than water changes is necessary to keep your values in check indefinitely.
But what does this really tell us? Perhaps if I do a 1 percent water change every week indefinitely, I will end up with just 0.01 nitrates or 8.199 pH. The formula doesn't say that this cannot happen and I would be perfectly okay with that value for nitrates or pH. So we simply take the original equation that we got from taking the limit and we set it equal to something else. Here, we set it equal to h plus or minus some error. We will add the error and just assume that the error can be negative depending on what we define the galloping elephant as (also note that when r is negative, so is e):

So if we set the value of e equal to 0, then we get the need for a 100% water change. As your willingness to accept error increases, the size of the water change that you need to do decreases. If any equation is potentially useful, it is this one. estimating your value for r and using your accepted error is a great way to ballpark the size of the water change you should be doing. Another method would be to vary the size of your water changes such that you are adding the necessary elements back into the aquarium. For example, doing the occasional giant water change could really help your system. Water changes are an important part of the hobby. It is important that we understand them and use them accordingly.
-Cameron