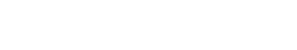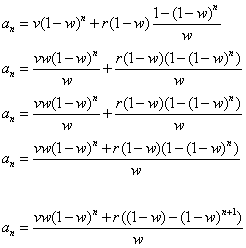pezenfuego
Active Member
I will begin by accrediting beaslbob for the original idea. His analogy involved galloping elephants, which were used as a general unit of measure. They can be easily replaced with other elements/molecules/levels in the aquarium. Specifically those that we wish to reach 0 (nitrates, phosphates, ammonia, nitrites)
I like the analogy, but I want to get a formula for this. So the question is this: "How important are water changes?" To answer this question we are going to begin with a few assumptions. As we proceed, we will eliminate these assumptions. We start by creating a formula for water changes. To use the formula, you will not need any sort of mathematical ability, but to follow the thread, you will need a very basic understanding of mathematics.
Assumption:
1) The aquarist knows exactly how much water is in their system.
2) The aquarist has constant husbandry
3) Galloping elephants are equally distributed throughout the water (if this is not a fair assumption, then we are improperly testing our water for galloping elephants).
4) Galloping elephants increase at a uniform rate (independent of water changes) that can be measured (the important part of this assumption is the increase portion. If they increase in such a way that is not uniform, this does not hinder the overall idea, but will render the formula itself useless).
5) Water changes are the only thing that can remove galloping elephants.
6) No galloping elephants were in the system to begin with (This assumption is almost never true, but we will tackle this problem later on)
The bolded assumptions are assumptions that I deem unfair. We will tackle them later. Keep the first bolded assumption in mind. It is the most important part of this thread.
Variables:
n= number of weeks
r= rate that galloping elephants increases each week
w= fraction of water that is replaced each week (0<w<1)
If you know these three variables, you can estimate the CHANGE in your water parameters throughout time and calculate how big of a water change you need to do (assuming r is uniform and positive). Go through this thread and if you get caught, reread it. It should be easy to understand, but may take some effort to follow.
So let's begin by figuring out this series. Here an=the amount of galloping elephants in the tank.
To begin, we know that

Because one of our assumption was that there were no galloping elephants in the water to begin with. So after a week (and before a water change) how many galloping elephants are in the water? That's also easy. The answer is r galloping elephants (as we gain r galloping elephants each week). Next we need to determine what a water change does. Since galloping elephants are equally distributed in the water, then removing w percent of the water will remove w percent of the galloping elephants. So:
forums.saltwaterfish.com/content/type/61/id/365626/">

is the amount of galloping elephants that are removed. So after 1 week and 1 water change, we get:
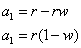
Now we wait another week. After another week, we have to add an additional r galloping elephants.
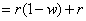
And our water change will remove w percent of these galloping elephants:
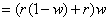
And the difference is:
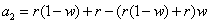
This form looks a little different than our a1 value, but we can rewrite it like this:
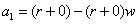
Recall that n is the number of weeks. We want to find a formula for any number of weeks. Then it becomes obvious that the general form of this is:
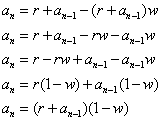
By plugging in 1 and 2, we see that this checks out for those values. This is the simplest form, but not the easiest to work with. So we revert a little bit. After doing that, we want to see if we can find a value for an that does not include an-1. We do this because an-1 is very difficult to work with.

Now, we want to represent this as a summation.
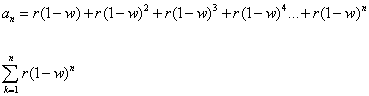
We don't want this as a summation though, we want this as an equation that we can easily plug values into. So we use the geometric series formula:
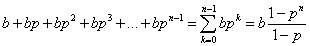
I will not provide a proof for this here. It is unnecessary and can be found easily online. It is important to note 2 things about this:
1. The variables that are usually used to represent this are a and r. However, because we are already using this variables, b and p are used to simplify things.
2. This is only true where the absolute value of p is less than 1. Since p is equal to 1-w and since w cannot be greater than or equal to 1 or less than 0, this does not present a problem (unless you attempt to plug in 0 for the value of w. If this is the case, you will have to take a limit. Fortunately, calculating these values without water changes is so easy, you don't need the formula in the first place).
But you will notice that our summation is different from the one we need to use. So we change it a little. This can be done in your head pretty easily:
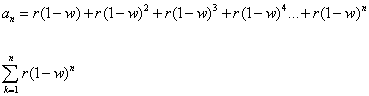
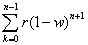
We know that to be true as shifting k=1 to k=0 forces us to shift the value of n to n+1 in the equation. But if we just leave it like that, then our series will end with the term r(1-w)^(n+1). That is not a good thing. We don't want that. So we must end our series at n-1 such that the last term is r(1-w)^n. Now that's what we want. So we have this equation, but it still isn't quite right because we can't evaluate that n+1. So we have to pull out a (1-w).
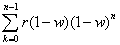
And we check it to make sure that what we did was valid:
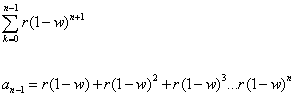
Well, that's the same as before, so we're good.
Now we have this in the form we need it in and can evaluate it using the geometric series.

So there is the formula...Let's test it (using something other than galloping elephants-how about nitrates?)
Ex:
1. A nitrate increase of 7 ppm per week
2. Over the course of 3 weeks
3. Doing a 20% water change per week (note that it may be easier to convert this to a fraction- e.g. 1/5)
And it comes back with...13.664 ppm
Is this reasonable? Well, let's assume that we don't do any water changes (ie w=0). If this was the case, then we would simply have r*n as our value. So we would end up with 21 ppm of nitrates. So the water changes reduced this but not by a whole lot.
So we are done with the first portion of the problem, but a big hole still remains. This only works when we don't have any galloping elephants to begin with. That is almost never the case. So we have to move on to part two.
Part 2
We will now tackle assumption number 5. Before we assumed 0 initial galloping elephants and a linear increase in galloping elephants (r). Now let's reverse that. We begin with some initial value of galloping elephants and assume that there is no increase in galloping elephants. Let's define our variables.
v=initial value of galloping elephants
w=percent water change
n= number of weeks
So the reduction of galloping elephants is given by:
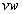
and of course the initial value of galloping elephants is v, so our equation after 1 week becomes:
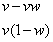
So we look at the first few terms:
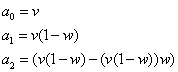
And the pattern becomes clear very quickly (as it is similar to the other one):
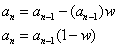
Then we test this to see if we get the same thing for the first few values.

We do! This is our equation. It is much simpler than before.
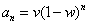
Now let's test this.
w=25% or (1/4)
v=30ppm nitrates
n=5 weeks
50/height/700" />
Here we see that the nitrates were reduced significantly in this five week period. We also notice that it will take an infinite amount of time to reach 0 and that we reduce it by less and less each time. Just something to note. So now the hard part comes. How do we take these two different equations and combine them so that we can determine the value of nitrates in the water with both a rate of increase and an initial value.
So how do we do that. It must be complicated, right?
Wrong, we just add the two equations. How do we justify that? Think about it. It is difficult to explain, so I'll just say this:
What is different about the galloping elephants that were in the tank initially and the galloping elephants that showed up over the course of time? The answer is nothing. So we can consider them together.
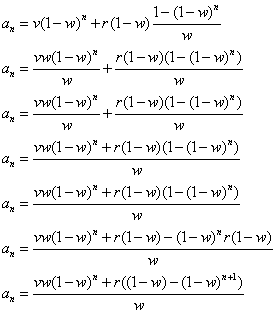
We have our formula. Since we did a lot of work and there is tons of room for error, let's test this for values that we know. Let's test to see what happens when we do a 100% water change.
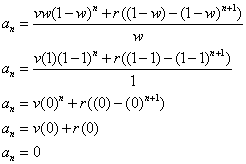
That makes sense. If we do 100% water changes, we should expect to have no galloping elephants in the water.
Now, we could test this for 0, but that wouldn't work because we decided to use the geometric series and that dictates that w cannot be 0.
So we could either find the limit as w approaches 0, or evaluate it for a very small value (a cop-out)
First let's define a few values.
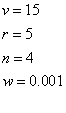
Plugging in these values we get:
34.89
Now, if we did a 0% water change each week, we would expect that the value for our galloping elephants would be the initial value plus the rate times the amount of time (n) that passes. In essence (rn+v) or (5*4+15) or 35. That means that this equation is correct. Now let's test it for some real values.
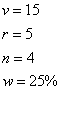
And we get 10.27ppm nitrates
Another question that might come up is "What if I don't do weekly water changes?" This same formula can be applied to daily, weekly, biweekly, etc. water changes. The units must be the same, but otherwise it will work. For example, if r is in terms of a day, then n must also be in terms of days.
Does this reflect reality? The answer to that is no. Why does it not reflect reality? We need to go back to the assumptions:
1) Galloping elephants increase at a uniform rate (independent of water changes) that can be measured
2) Water changes are the only thing that can remove galloping elephants.
3) No galloping elephants were in the system to begin with.
We can eliminate assumption 3 because we have already handled it. Now, we assumptions 2 and 3 cannot be dealt with. There is no way to deal with the other two. Does that render everything we just did useless? No, it doesn't. Remember the point of this thread was not to create a formula that can predict galloping elephant levels throughout time. The point of this thread was to examine how useful water changes are. We can still achieve this goal even with our faulty assumptions. We can combine the two assumptions and realize that if we assume nothing else can remove galloping elephants, then (r) can only increase or be 0. That is the important bit, we don't particularly care if galloping elephants increase at an exponential or geometric rate; and we don't care if these rates are constant. As long as they are increasing, we can trudge on.
Okay, so let's examine the second assumption more closely. We do this by taking our formula and seeing what the value for an is after an infinite number of weeks. In other words, our question is "Will my galloping elephant count ever reach 0 with water changes?" We do that by taking the limit of the equation as n approaches infinity.
Just by looking at the equation, it appears as though an approaches infinity, but that is not the case. Let's look at this rule:
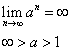
This is true, and somewhat intuitive. Now let's look at this for (1/a)
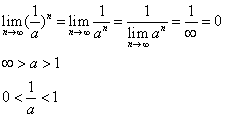
Basically what this proves is that when a is greater than 1, the answer is infinity. But when a is a fraction, the answer is 0. The value that we are raising to the power of n is (1-w) and we know that w is between the values of 0 and 1, so we look at how (1-w) behaves:
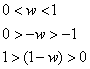
Interestingly, it behaves the same was as w and more importantly, it behaves the same way as (1/a)
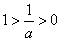
So that proves this:
"https://forums.saltwaterfish.com/data/9/98/980fcbbc_33.gif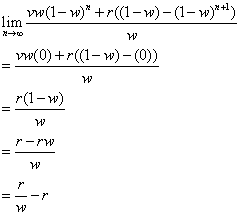
Now we have an equation for this and there are two things that I want to recognize. The first is that this equation does not rely on the value for v. That is important to realize and it shows that water changes do help the system. The question then becomes, at what values of w will we end up with 0 galloping elephants?
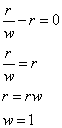
We will only get to 0 galloping elephants when we do 100% water changes. But that is not entirely true as it relies on this assumption:
Water changes are the only thing that can remove galloping elephants
What have we mathematically proven? Simply put:
In order to get our galloping elephant count to 0, we cannot rely solely on water changes.
Here is where the analogy gets extended. If we cannot rely solely on water changes, then what do we for our system? The answer is to add pouncing lions to our system to eat the galloping elephants.
What are pouncing lions? Pouncing lions is an analogy for anything except water changes that can remove galloping elephants. Things things include, but are not limited to, protein skimmers (perhaps aided by vodka or vinegar dosing), turf scrubbers, natural and chemical filtration, macroalgae, and deep sand beds.
These things have the potential to get your galloping elephant count to 0 and water changes can help.
It is also worth mentioning that there are other chemicals in the aquarium which cannot be considered galloping elephants (sodium, potassium, calcium, etc). These things can be thought of as the opposite of galloping elephants. We want them in our tank and our tank consumes them. That is the extent of the galloping elephant analogy. Water changes are important to keep these levels in balance, but if we flip the idea, it logically follows that eventually we will have to add these elements via dosing. But we cannot dose for everything, which renders water changes essential. It also shows that in order to keep your system in balance indefinitely, a very large water change (much closer to 100% than your regular water changes) is essential on occasion. How often you do this is dependent on your system. Perhaps you will never need to do this as your levels will never fall below what is acceptable in your lifetime.
-Cameron
I like the analogy, but I want to get a formula for this. So the question is this: "How important are water changes?" To answer this question we are going to begin with a few assumptions. As we proceed, we will eliminate these assumptions. We start by creating a formula for water changes. To use the formula, you will not need any sort of mathematical ability, but to follow the thread, you will need a very basic understanding of mathematics.
Assumption:
1) The aquarist knows exactly how much water is in their system.
2) The aquarist has constant husbandry
3) Galloping elephants are equally distributed throughout the water (if this is not a fair assumption, then we are improperly testing our water for galloping elephants).
4) Galloping elephants increase at a uniform rate (independent of water changes) that can be measured (the important part of this assumption is the increase portion. If they increase in such a way that is not uniform, this does not hinder the overall idea, but will render the formula itself useless).
5) Water changes are the only thing that can remove galloping elephants.
6) No galloping elephants were in the system to begin with (This assumption is almost never true, but we will tackle this problem later on)
The bolded assumptions are assumptions that I deem unfair. We will tackle them later. Keep the first bolded assumption in mind. It is the most important part of this thread.
Variables:
n= number of weeks
r= rate that galloping elephants increases each week
w= fraction of water that is replaced each week (0<w<1)
If you know these three variables, you can estimate the CHANGE in your water parameters throughout time and calculate how big of a water change you need to do (assuming r is uniform and positive). Go through this thread and if you get caught, reread it. It should be easy to understand, but may take some effort to follow.
So let's begin by figuring out this series. Here an=the amount of galloping elephants in the tank.
To begin, we know that

Because one of our assumption was that there were no galloping elephants in the water to begin with. So after a week (and before a water change) how many galloping elephants are in the water? That's also easy. The answer is r galloping elephants (as we gain r galloping elephants each week). Next we need to determine what a water change does. Since galloping elephants are equally distributed in the water, then removing w percent of the water will remove w percent of the galloping elephants. So:
forums.saltwaterfish.com/content/type/61/id/365626/">

is the amount of galloping elephants that are removed. So after 1 week and 1 water change, we get:
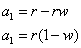
Now we wait another week. After another week, we have to add an additional r galloping elephants.
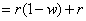
And our water change will remove w percent of these galloping elephants:
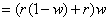
And the difference is:
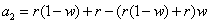
This form looks a little different than our a1 value, but we can rewrite it like this:
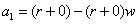
Recall that n is the number of weeks. We want to find a formula for any number of weeks. Then it becomes obvious that the general form of this is:
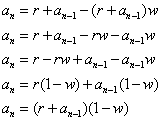
By plugging in 1 and 2, we see that this checks out for those values. This is the simplest form, but not the easiest to work with. So we revert a little bit. After doing that, we want to see if we can find a value for an that does not include an-1. We do this because an-1 is very difficult to work with.

Now, we want to represent this as a summation.
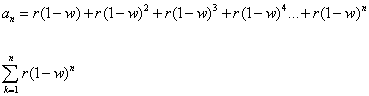
We don't want this as a summation though, we want this as an equation that we can easily plug values into. So we use the geometric series formula:
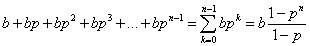
I will not provide a proof for this here. It is unnecessary and can be found easily online. It is important to note 2 things about this:
1. The variables that are usually used to represent this are a and r. However, because we are already using this variables, b and p are used to simplify things.
2. This is only true where the absolute value of p is less than 1. Since p is equal to 1-w and since w cannot be greater than or equal to 1 or less than 0, this does not present a problem (unless you attempt to plug in 0 for the value of w. If this is the case, you will have to take a limit. Fortunately, calculating these values without water changes is so easy, you don't need the formula in the first place).
But you will notice that our summation is different from the one we need to use. So we change it a little. This can be done in your head pretty easily:
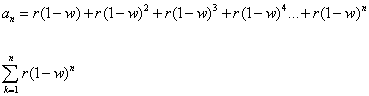
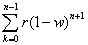
We know that to be true as shifting k=1 to k=0 forces us to shift the value of n to n+1 in the equation. But if we just leave it like that, then our series will end with the term r(1-w)^(n+1). That is not a good thing. We don't want that. So we must end our series at n-1 such that the last term is r(1-w)^n. Now that's what we want. So we have this equation, but it still isn't quite right because we can't evaluate that n+1. So we have to pull out a (1-w).
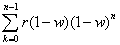
And we check it to make sure that what we did was valid:
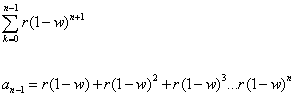
Well, that's the same as before, so we're good.
Now we have this in the form we need it in and can evaluate it using the geometric series.

So there is the formula...Let's test it (using something other than galloping elephants-how about nitrates?)
Ex:
1. A nitrate increase of 7 ppm per week
2. Over the course of 3 weeks
3. Doing a 20% water change per week (note that it may be easier to convert this to a fraction- e.g. 1/5)
And it comes back with...13.664 ppm
Is this reasonable? Well, let's assume that we don't do any water changes (ie w=0). If this was the case, then we would simply have r*n as our value. So we would end up with 21 ppm of nitrates. So the water changes reduced this but not by a whole lot.
So we are done with the first portion of the problem, but a big hole still remains. This only works when we don't have any galloping elephants to begin with. That is almost never the case. So we have to move on to part two.
Part 2
We will now tackle assumption number 5. Before we assumed 0 initial galloping elephants and a linear increase in galloping elephants (r). Now let's reverse that. We begin with some initial value of galloping elephants and assume that there is no increase in galloping elephants. Let's define our variables.
v=initial value of galloping elephants
w=percent water change
n= number of weeks
So the reduction of galloping elephants is given by:
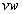
and of course the initial value of galloping elephants is v, so our equation after 1 week becomes:
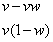
So we look at the first few terms:
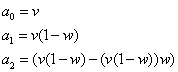
And the pattern becomes clear very quickly (as it is similar to the other one):
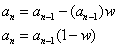
Then we test this to see if we get the same thing for the first few values.

We do! This is our equation. It is much simpler than before.
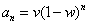
Now let's test this.
w=25% or (1/4)
v=30ppm nitrates
n=5 weeks
50/height/700" />
Here we see that the nitrates were reduced significantly in this five week period. We also notice that it will take an infinite amount of time to reach 0 and that we reduce it by less and less each time. Just something to note. So now the hard part comes. How do we take these two different equations and combine them so that we can determine the value of nitrates in the water with both a rate of increase and an initial value.
So how do we do that. It must be complicated, right?
Wrong, we just add the two equations. How do we justify that? Think about it. It is difficult to explain, so I'll just say this:
What is different about the galloping elephants that were in the tank initially and the galloping elephants that showed up over the course of time? The answer is nothing. So we can consider them together.
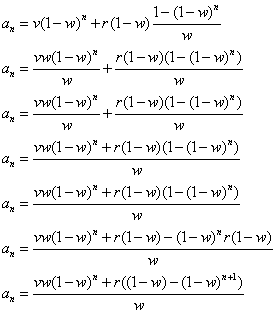
We have our formula. Since we did a lot of work and there is tons of room for error, let's test this for values that we know. Let's test to see what happens when we do a 100% water change.
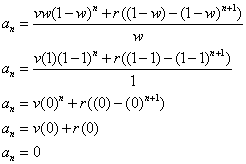
That makes sense. If we do 100% water changes, we should expect to have no galloping elephants in the water.
Now, we could test this for 0, but that wouldn't work because we decided to use the geometric series and that dictates that w cannot be 0.
So we could either find the limit as w approaches 0, or evaluate it for a very small value (a cop-out)
First let's define a few values.
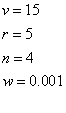
Plugging in these values we get:
34.89
Now, if we did a 0% water change each week, we would expect that the value for our galloping elephants would be the initial value plus the rate times the amount of time (n) that passes. In essence (rn+v) or (5*4+15) or 35. That means that this equation is correct. Now let's test it for some real values.
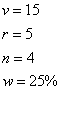
And we get 10.27ppm nitrates
Another question that might come up is "What if I don't do weekly water changes?" This same formula can be applied to daily, weekly, biweekly, etc. water changes. The units must be the same, but otherwise it will work. For example, if r is in terms of a day, then n must also be in terms of days.
Does this reflect reality? The answer to that is no. Why does it not reflect reality? We need to go back to the assumptions:
1) Galloping elephants increase at a uniform rate (independent of water changes) that can be measured
2) Water changes are the only thing that can remove galloping elephants.
3) No galloping elephants were in the system to begin with.
We can eliminate assumption 3 because we have already handled it. Now, we assumptions 2 and 3 cannot be dealt with. There is no way to deal with the other two. Does that render everything we just did useless? No, it doesn't. Remember the point of this thread was not to create a formula that can predict galloping elephant levels throughout time. The point of this thread was to examine how useful water changes are. We can still achieve this goal even with our faulty assumptions. We can combine the two assumptions and realize that if we assume nothing else can remove galloping elephants, then (r) can only increase or be 0. That is the important bit, we don't particularly care if galloping elephants increase at an exponential or geometric rate; and we don't care if these rates are constant. As long as they are increasing, we can trudge on.
Okay, so let's examine the second assumption more closely. We do this by taking our formula and seeing what the value for an is after an infinite number of weeks. In other words, our question is "Will my galloping elephant count ever reach 0 with water changes?" We do that by taking the limit of the equation as n approaches infinity.
Just by looking at the equation, it appears as though an approaches infinity, but that is not the case. Let's look at this rule:
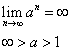
This is true, and somewhat intuitive. Now let's look at this for (1/a)
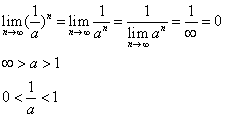
Basically what this proves is that when a is greater than 1, the answer is infinity. But when a is a fraction, the answer is 0. The value that we are raising to the power of n is (1-w) and we know that w is between the values of 0 and 1, so we look at how (1-w) behaves:
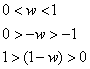
Interestingly, it behaves the same was as w and more importantly, it behaves the same way as (1/a)
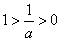
So that proves this:
"https://forums.saltwaterfish.com/data/9/98/980fcbbc_33.gif
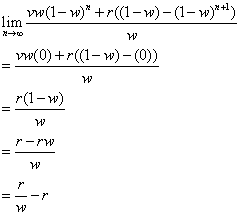
Now we have an equation for this and there are two things that I want to recognize. The first is that this equation does not rely on the value for v. That is important to realize and it shows that water changes do help the system. The question then becomes, at what values of w will we end up with 0 galloping elephants?
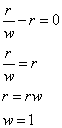
We will only get to 0 galloping elephants when we do 100% water changes. But that is not entirely true as it relies on this assumption:
Water changes are the only thing that can remove galloping elephants
What have we mathematically proven? Simply put:
In order to get our galloping elephant count to 0, we cannot rely solely on water changes.
Here is where the analogy gets extended. If we cannot rely solely on water changes, then what do we for our system? The answer is to add pouncing lions to our system to eat the galloping elephants.
What are pouncing lions? Pouncing lions is an analogy for anything except water changes that can remove galloping elephants. Things things include, but are not limited to, protein skimmers (perhaps aided by vodka or vinegar dosing), turf scrubbers, natural and chemical filtration, macroalgae, and deep sand beds.
These things have the potential to get your galloping elephant count to 0 and water changes can help.
It is also worth mentioning that there are other chemicals in the aquarium which cannot be considered galloping elephants (sodium, potassium, calcium, etc). These things can be thought of as the opposite of galloping elephants. We want them in our tank and our tank consumes them. That is the extent of the galloping elephant analogy. Water changes are important to keep these levels in balance, but if we flip the idea, it logically follows that eventually we will have to add these elements via dosing. But we cannot dose for everything, which renders water changes essential. It also shows that in order to keep your system in balance indefinitely, a very large water change (much closer to 100% than your regular water changes) is essential on occasion. How often you do this is dependent on your system. Perhaps you will never need to do this as your levels will never fall below what is acceptable in your lifetime.
-Cameron